不同构型旋翼无人机的控制

摘要：讨论由多组倾转或固定旋翼驱动的单一刚体无人机的姿态/位置轨迹跟踪控制。包含的无人机类型有：正X型四旋翼(Quadcopter)，倾转三旋翼(Tricopter)，倾转双旋翼(Bicopter)，矢量共轴双旋翼(Singlecopter)，全驱动倾转三旋翼，全驱动六旋翼。

1 不同构型旋翼无人机的控制

 考虑由多组倾转或者固定电机驱动的单一刚体旋翼无人机，有如下假设：

• 忽略螺旋桨、电机转子的质量和转动惯量，即除了螺旋桨提供升力和反作用力矩，其他附加的惯性力和科氏力都忽略不计。
• 对于倾转旋翼，忽略倾转舵机的响应时间，即假设控制过程中舵机能够快速到达指定角度。
• 忽略其他空气动力学因素产生的作用力。
• 无人机的重心和质心重合，即重力的作用不会使机体发生旋转。
• 不考虑环境扰动。

则旋翼无人机控制问题可以被简化为一个刚体的控制问题，对于给定的期望轨迹和测量得到的状态量，基于简化的刚体动力学，设计位置和姿态控制器，得到期望的机体作用力和力矩，再结合无人机构型，计算电机的混控，由位置和姿态控制的输入计算期望电机输出和舵机转角。其大致的控制流程如图所示。

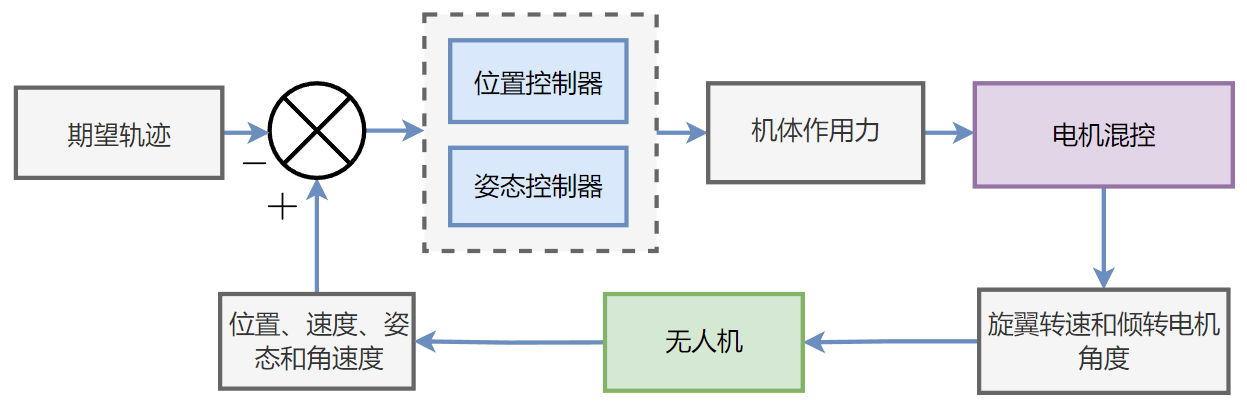
需要说明的是：上述假设与实际情况有比较大的差异，但是如果无人机的构型对简化的建模不是特别敏感(各种建模不确定性满足李普希茨条件)的话，利用控制器的高增益，也是能够达到不错的控制效果的。如果需要更好的控制性能，则需要更少的假设，更精确的建模，使用性能更好的控制器等。

1.1 单一刚体的动力学和控制

 根据牛顿-欧拉法，简化成单一刚体的无人机动力学可以表示为：

$$\begin{align} &\dot{\boldsymbol{p}}=\boldsymbol{v}\tag{1.1}\\ &\dot{\boldsymbol{v}}=M^{-1}R\boldsymbol{f}-g\boldsymbol{e}_3\tag{1.2}\\ &\dot{R}=R\mathrm{sk}(\boldsymbol{\omega})\tag{1.3}\\ &\dot{\boldsymbol{\omega}}=J^{-1}(-\boldsymbol{\omega}\times J\boldsymbol{\omega}+\boldsymbol{\tau}) \tag{1.4} \end{align}$$

其中：

• $\boldsymbol{p}\in\mathbb{R}^3$和$\boldsymbol{v}\in\mathbb{R}^3$分别为无人机在绝对坐标系下的位置和速度。
• $M\in\mathbb{R}$和$J\in\mathbb{R}^{3\times3}$分别为无人机的质量和惯性矩阵。
• $R\in SO(3)$为无人机的姿态旋转矩阵。
• $g$为重力加速度，$\boldsymbol{e}_3=[0,0,1]^{\mathrm{T}}$。
• $\boldsymbol{\omega}$为无人机角速度在机体坐标系下的表示。
• $\boldsymbol{f}\in\mathbb{R}^3$和$\boldsymbol{\tau}\in\mathbb{R}^3$分别为无人机所受力和力矩在机体坐标系下的表示。

上述动力学中，位置和速度的表示是在绝对坐标系下，角速度的表示则在机体坐标系下。这主要是考虑到实际应用中，传感器测量得到的通常是绝对坐标系下的位置和速度(GPS)，以及机体坐标系下的角速度(IMU)。根据表示状态量的坐标系的不同，动力学的表示也会有所差异。

 本文中涉及的无人机可分为非完整约束欠驱动和全驱动两类。对于欠驱动无人机，$\boldsymbol{f}$和$\boldsymbol{\tau}$中存在元素为零或者相互耦合的量，因此在控制中不能全部作为系统的输入，需要结合受控对象选择需要控制的状态量和控制输入。例如平面四旋翼无人机，四个旋翼不能提供机体侧向力，即$\boldsymbol{f}=[0,0,f_z]^{\mathrm{T}}$，为了实现3个自由度的位置控制，需要将$R\boldsymbol{f}$作为位置环的控制输入，再根据这一输入解算出期望的姿态$R$和升力$f_z$，设计姿态控制器进行跟踪。对于全驱动的无人机，$\boldsymbol{f}$和$\boldsymbol{\tau}$总共有六个互相正交的量，每个量都可以独立输入，因此可以将$\boldsymbol{f}$和$\boldsymbol{\tau}$作为系统的输入，分别控制无人机的6个自由度。

 对于位置控制器，这里初步将$R\boldsymbol{f}$作为控制输入给出一个能够收敛的控制器。定义期望轨迹为$\boldsymbol{p}_d$，误差$\boldsymbol{e}=\boldsymbol{p}-\boldsymbol{p}_d$，则关于控制误差的位置动力学可以写作：

$$\ddot{\boldsymbol{e}}=M^{-1}R\boldsymbol{f}-g\boldsymbol{e}_3-\ddot{\boldsymbol{p}}_d \tag{1.5}$$

设计控制器为：

$$R\boldsymbol{f}=M(-k_p\boldsymbol{e}-k_d\dot{\boldsymbol{\boldsymbol{e}}}+g\boldsymbol{e}_3+\ddot{\boldsymbol{p}}_d) \tag{1.6}$$

则闭环动力学可以写作：

$$\ddot{\boldsymbol{e}}+k_d\dot{\boldsymbol{e}}+k_p\boldsymbol{e}=0 \tag{1.7}$$

利用二阶线性常系数齐次微分方程的解，可知，当$k_p,k_d>0$且$k_d^2-4k_p>0$时，上述微分方程对应的特征根方程有两个负实数解:$r_1,r_2<0$，微分方程的解为$\boldsymbol{e}=C_1\exp(r_1t)+C_2\exp(r_2t)$，当$t\rightarrow\infty$时$\boldsymbol{e}\rightarrow0$。
 对于姿态控制，可参考 刚体姿态控制。

 基于设计好控制器，可以计算出控制无人机所需的机体作用力$\boldsymbol{f}$和作用力矩$\boldsymbol{\tau}$，再利用无人机的混控关系求得旋翼的转速和倾转电机的角度。

1.2 电机混控

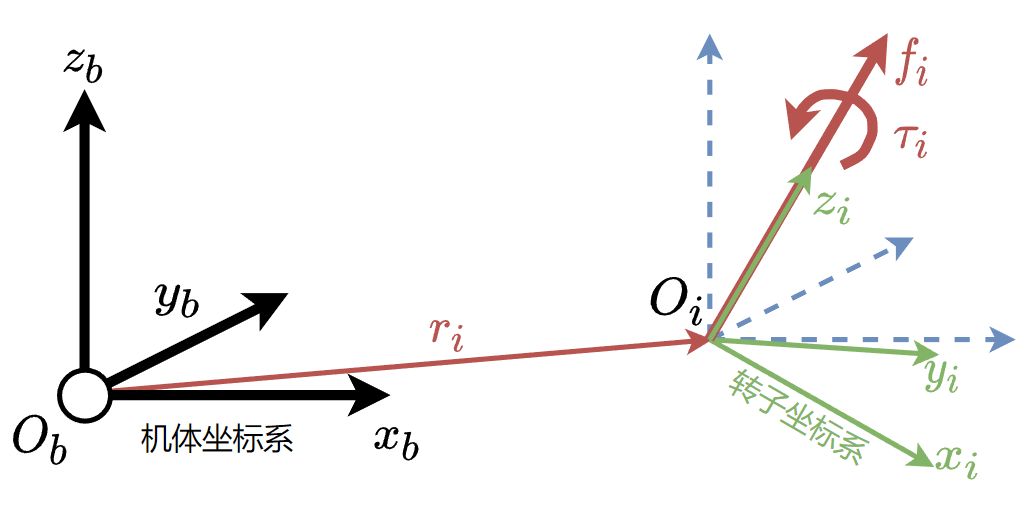
 无人机每个旋翼提供的升力和反作用力矩如图所示。定义第$i$个螺旋桨的转子坐标系为$R_i$，转子坐标系的$z$轴与电机轴重合。记第$i$个螺旋桨提供的升力和反作用力矩分别$f_i$和$\tau_i$，对于逆时针(CCW)旋转的螺旋桨反作用力矩为负，对于顺时针(CW)旋转的桨反作用力矩为正。$f_i$和$\tau_i$与螺旋桨转速$\omega_i$的关系可以近似为：

$$\begin{aligned} &f_i=C_f\omega^2_i\\ &\tau_i=aC_{\tau}\omega^2_i \end{aligned}\tag{1.8}$$

其中$C_f$和$C_{\tau}$是与空气动力学参数相关的系数。$a$表示螺旋桨的旋向，当螺旋桨逆时针(CCW)旋转时，$a=-1$；当螺旋桨顺时针(CW)旋转时，$a=1$。因此可以将$\tau_i$记作：

$$\tau_i=akf_i \tag{1.9}$$

其中$k=C_{\tau}/C_f。$考虑到利用公式就可由升力求得对应的螺旋桨转速，为了简便书写，后续的推导将以螺旋桨的升力作为控制输入。

 第$i$个螺旋桨在作用点处的力和力矩在机体坐标系下的表示为：

$$\begin{align} &F_i=R_i[0,0,f_i]^{\mathrm{T}} \tag{1.10}\\ &M_i=R_i[0,0,akf_i]^{\mathrm{T}} \tag{1.11} \end{align}$$

将所有力和力矩向质心简化，$n$个螺旋桨提供的合力在机体坐标系下的表示为：

$$\begin{align} &\boldsymbol{f}=\sum^{n}_{i=1}F_i \tag{1.12}\\ &\boldsymbol{\tau}=\sum^{n}_{i=1}\boldsymbol{r}_i\times F_i+M_i \tag{1.13} \end{align}$$

其中$\boldsymbol{r}_i$为机体质心到螺旋桨受力点的位置矢量。解(1.11)和(1.12)，就可以由控制输入$\boldsymbol{f}$和$\boldsymbol{\tau}$计算每个螺旋桨的升力和倾转电机的角度。

2 欠驱动无人机

2.1 平面四旋翼(正X型-Qaudcopter)

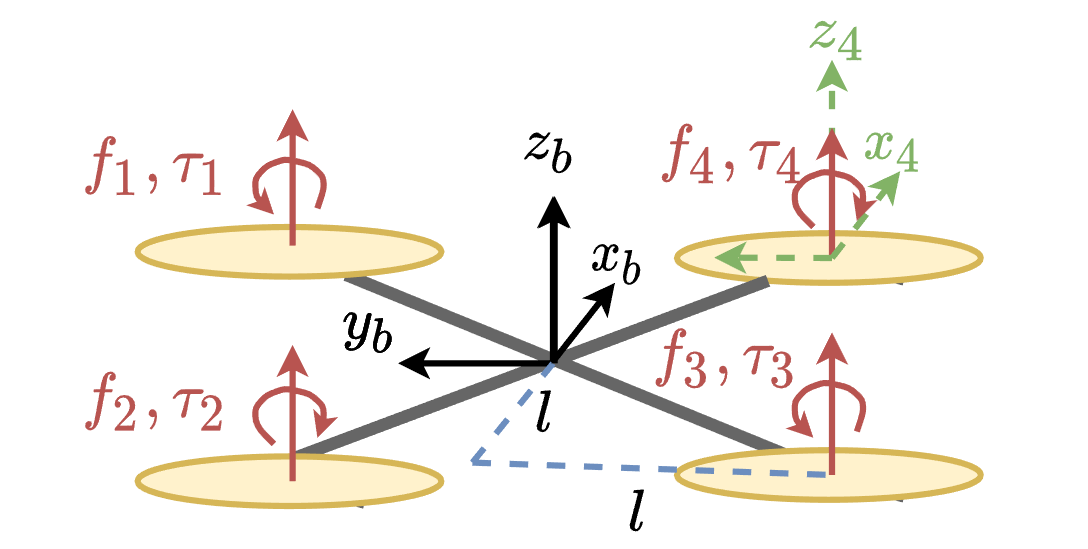
 如图所示，选取螺旋桨1和3产生的反作用力矩为正，螺旋桨2和4产生的反作用力矩为负(力矩的正负可以用右手定则判断)。每个螺旋桨到坐标系x轴和y轴的距离都为$l$。首先，利用第一章中的公式来推导混控矩阵，可以列出以下关系：

$$R_1=R_2=R_3=R_4=\mathrm{diag}(1,1,1)\tag{2.1}$$ $$\begin{aligned} &F_1=R_1[0,0,f_1]^{\mathrm{T}},&M_1&=R_1[0,0,kf_1]^{\mathrm{T}}\\ &F_2=R_2[0,0,f_2]^{\mathrm{T}},&M_2&=R_2[0,0,-kf_2]^{\mathrm{T}}\\ &F_3=R_3[0,0,f_3]^{\mathrm{T}},&M_3&=R_3[10,0,kf_3]^{\mathrm{T}}\\ &F_4=R_4[0,0,f_4]^{\mathrm{T}},&M_4&=R_4[0,0,-kf_4]^{\mathrm{T}} \end{aligned}\tag{2.2}$$ $$\begin{aligned} &\boldsymbol{r}_1=[l,l,0]^{\mathrm{T}}\\ &\boldsymbol{r}_2=[-l,l,0]^{\mathrm{T}}\\ &\boldsymbol{r}_3=[-l,-l,0]^{\mathrm{T}}\\ &\boldsymbol{r}_4=[l,-l,0]^{\mathrm{T}} \end{aligned}\tag{2.3}$$

根据公式(1.12)和(1.13)可以得到：

$$\boldsymbol{f}=\begin{bmatrix} 0\\ 0\\ f_1+f_2+f_3+f_4 \end{bmatrix},~\boldsymbol{\tau}=\begin{bmatrix} lf_1+lf_2-lf_3-lf_4\\ -lf_1+lf_2+lf_3-lf_4\\\ kf_1-kf_2+kf_3-kf_4 \end{bmatrix}\tag{2.4}$$

记$\boldsymbol{f}=[f_x,f_y,f_z]^{\mathrm{T}}$和$\boldsymbol{\tau}_b=[\tau_x,\tau_y,\tau_z]^{\mathrm{T}}$，可以写成矩阵形式：

$$\begin{bmatrix} f_z\\ \tau_x\\ \tau_y\\ \tau_z \end{bmatrix}=\begin{bmatrix} 1&1&1&1\\ l&l&-l&-l\\ -l&l&l&-l\\ k&-k&k&-k \end{bmatrix}\begin{bmatrix} f_1\\ f_2\\ f_3\\ f_4 \end{bmatrix}\tag{2.5}$$

对公式(2.5)求逆可以得到：

$$\begin{bmatrix} f_1\\ f_2\\ f_3\\ f_4 \end{bmatrix}=\frac{1}{4lk}\begin{bmatrix} lk&k&-k&l\\ lk&k&k&-l\\ lk&-k&k&l\\ lk&-k&-k&-l \end{bmatrix}\begin{bmatrix} f_z\\ \tau_x\\ \tau_y\\ \tau_z \end{bmatrix}\tag{2.6}$$

 可以看出四旋翼无人机无法提供侧向的机体作用力，需要将期望姿态作为位置控制器的输入以实现三个自由度的位置控制。对于公式(1.6)中的设计的位置控制器，将等式右边计算出来的控制量记作：$\boldsymbol{u}=[u_x,u_y,u_z]^{\mathrm{T}}$，当期望姿态满足如下公式时，根据1.1中的推导，位置控制器能够收敛：

$$R^*\begin{bmatrix} 0\\ 0\\ f_z \end{bmatrix}=\begin{bmatrix} u_x\\ u_y\\ u_z \end{bmatrix}\tag{2.7}$$

其中$R^{\star}$为期望姿态。
定义$R^{\star}=[\boldsymbol{n}_1,\boldsymbol{n}_2,\boldsymbol{n}_3]$，其中 $\boldsymbol{n}_i$为三维列向量，则根据(2.8)可以解得期望的姿态和升力：

$$\begin{aligned} &f_z=||\boldsymbol{u}||\\ &\boldsymbol{n}_1=\boldsymbol{n}_2\times\boldsymbol{n}_3\\ &\boldsymbol{n}_2=\frac{\boldsymbol{n}_3\times\boldsymbol{h}}{||\boldsymbol{n}_3\times\boldsymbol{h}||}\\ &\boldsymbol{n}_3=\frac{\boldsymbol{u}}{||\boldsymbol{u}||} \end{aligned} \tag{2.8}$$

其中$\boldsymbol{h}=[\mathrm{cos}{\psi}^{\star},\mathrm{cos}{\psi}^{\star},0]^{\mathrm{T}}$，$\psi^{\star}$为无人机的期望偏航角。最后设计姿态控制器跟踪$R^{\star}$就实现四旋翼无人机的控制了，可以参考 刚体姿态控制。四旋翼无人机的控制流程图大致如下：

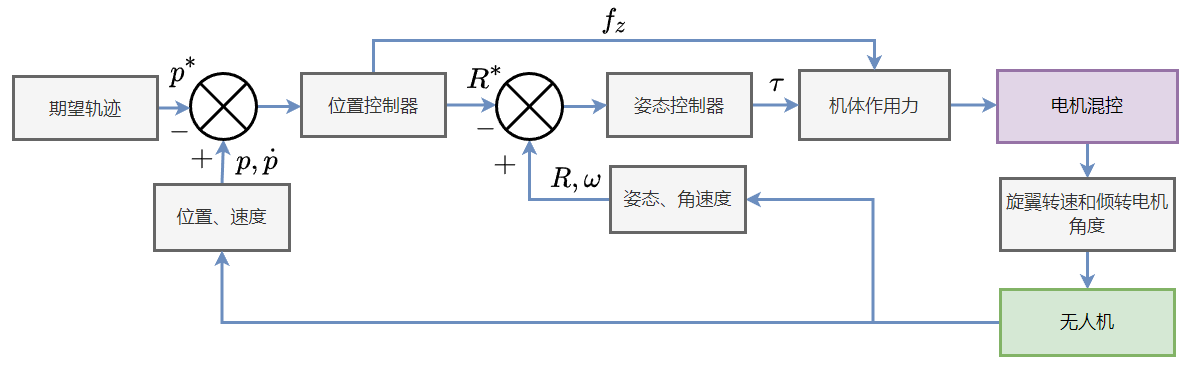
ps：这种位置和姿态串级控制的这种方式，建立在内外环分离假设的基础上，即假设姿态环是0误差跟踪的。因此在应用中，要求内环的响应速度要高于外环。此外，由于外环的控制输入是内环的跟踪期望，因而内环的控制中会涉及高阶的状态量(姿态的跟踪需要$R^{\star}$和$\boldsymbol{\omega}^{\star}$，位置控制器中$R^*$与$\dot{\boldsymbol{e}}$相关，因此$\boldsymbol{\omega}^{\star}$会与$\ddot{\boldsymbol{e}}$有关)，如果使用差分来求取完整的内环期望轨迹$R^{\star}$和$\boldsymbol{\omega}^{\star}$，会导致误差和噪声被放大。在实现中可以省略内环期望的高阶项或者使用滤波器平滑外环的控制输入，即假设内环期望信号的高阶量是慢变或有界的。
 由位置控制器和姿态控制器可以求出无人机控制所需的机体升力和力矩$f_z,\tau_x,\tau_y,\tau_z$，再代入公式(2.6)可以求得四个旋翼的升力。

2.2 三旋翼(Tri-copter)

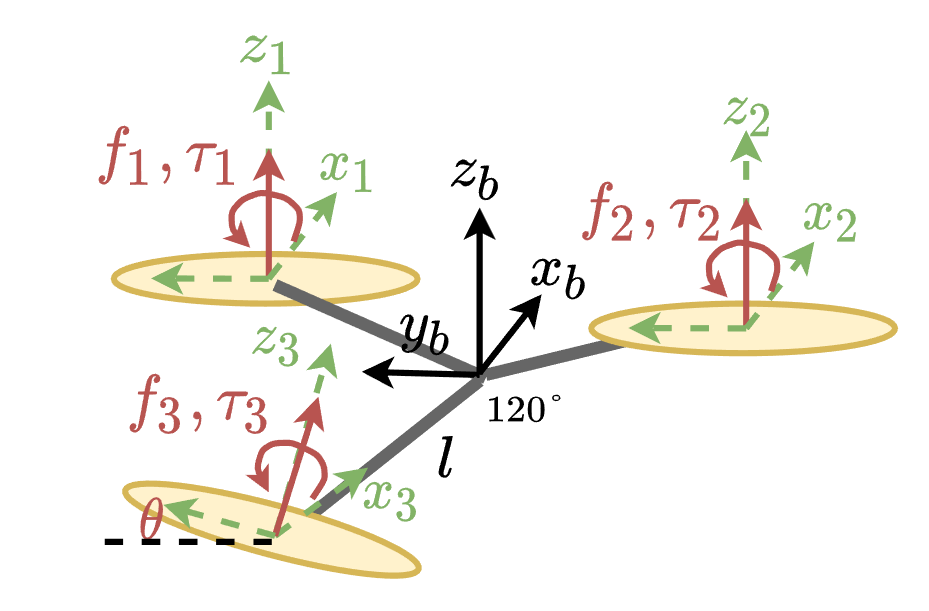
 三个旋翼产生的升力和反作用力矩方向如图所示，3号旋翼为倾转旋翼，倾转角度为$\theta$，机架为正三角形布置，机臂长为$l$。与四旋翼的步骤一样，先推导混控矩阵，可以列出：

$$\begin{aligned} &R_1=R_2=\mathrm{diag}(1,1,1)\\ &R_3=\mathrm{Rot}_x(\theta)=\begin{bmatrix} 1 & 0 &0 \\ 0 & \mathrm{cos}\theta &-\mathrm{sin}\theta \\ 0 & \mathrm{sin}\theta& \mathrm{cos}\theta \end{bmatrix} \end{aligned}\tag{2.9}$$ $$\begin{aligned} &F_1=R_1[0,0,f_1]^{\mathrm{T}},&M_1&=R_1[0,0,kf_1]^{\mathrm{T}}\\ &F_2=R_2[0,0,f_2]^{\mathrm{T}},&M_2&=R_2[0,0,kf_2]^{\mathrm{T}}\\ &F_3=R_3[0,0,f_3]^{\mathrm{T}},&M_3&=R_3[0,0,kf_3]^{\mathrm{T}}\\ \end{aligned}\tag{2.10}$$ $$\begin{aligned} &\boldsymbol{r}_1=\frac{1}{2}[l,\sqrt{3}l,0]^{\mathrm{T}}\\ &\boldsymbol{r}_2=\frac{1}{2}[l,-\sqrt{3}l,0]^{\mathrm{T}}\\ &\boldsymbol{r}_3=[-l,0,0]^{\mathrm{T}} \end{aligned}\tag{2.11}$$

根据公式(1.12)和(1.13)可以得到：

$$\boldsymbol{f}_b=\begin{bmatrix} 0\\ -f_3\mathrm{sin}\theta\\ f_1+f_2+f_3\mathrm{cos}\theta \end{bmatrix},~\boldsymbol{\tau}_b=\begin{bmatrix} \frac{\sqrt{3}}{2}lf_1 - \frac{\sqrt{3}}{2}lf_2\\ lf_3\mathrm{cos}\theta - \frac{1}{2}lf_1 - \frac{1}{2}lf_2 - kf_3\mathrm{sin}\theta\\\ kf_3\mathrm{cos}\theta + kf_1 + kf_2 + lf_3\mathrm{sin}\theta \end{bmatrix}\tag{2.12}$$

可以看出无人机受力与待求的$f_1,f_2,f_3,\theta$之间不是线型关系，可以先将$f_3\mathrm{cos}\theta$和$f_3\mathrm{sin}\theta$作为待求量，将上式写成矩阵形式：

$$\begin{bmatrix} f_y\\ f_z\\ \tau_x\\ \tau_y\\ \tau_z \end{bmatrix}=\begin{bmatrix} 0&0&0&-1\\ 1&1&1&0\\ \frac{\sqrt{3}}{2}l&-\frac{\sqrt{3}}{2}l&0&0\\ -\frac{1}{2}l&-\frac{1}{2}l&l&-k\\ k&k&k&l \end{bmatrix}\begin{bmatrix} f_1\\ f_2\\ f_3\mathrm{cos}\theta\\ f_3\mathrm{sin}\theta \end{bmatrix}\tag{2.13}$$

考虑到Tri-copter无人机只有4个可以驱动的量，因此$f_y=-f_3\mathrm{sin}\theta$为附加作用力，考虑到倾转电机工作的角度通常不会太大，因此这里假设$f_y\approx0$。解公式(2.13)可以得到：

$$\begin{bmatrix} f_1\\ f_2\\ f_3\mathrm{cos}\theta\\ f_3\mathrm{sin}\theta \end{bmatrix} =\frac{1}{3l^2}\begin{bmatrix}k^{2} + l^{2} & \sqrt{3}l & - l & -k\\ k^{2} + l^{2} & - \sqrt{3}l & -l & -k\\ -2k^{2} + l^{2} & 0 & 2l & 2k\\ -3kl & 0 & 0 & 3l\end{bmatrix}\begin{bmatrix} f_z\\ \tau_x\\ \tau_y\\ \tau_z \end{bmatrix}\tag{2.14}$$

 得到混控矩阵后，可以看出Tri-copter的位置和姿态控制器的输入与四旋翼是一样的，其余步骤代入四旋翼的控制流程即可。

2.3 倾转双旋翼(Bi-copter)

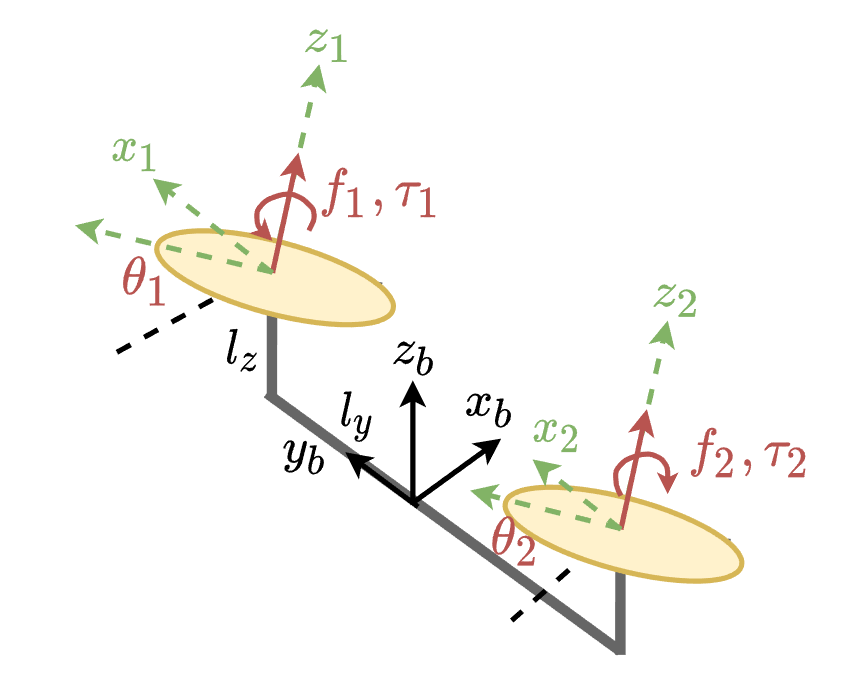
 Bi-copter的两个旋翼产生的机体作用力和力矩如图所示，倾转电机的角度分别为$\theta_1$和$\theta_2$，单机臂长为$l_y$，旋翼距离质心的高度为$l_z$，可以列出：

$$\begin{aligned} &R_1=\mathrm{Rot}_z(\frac{\pi}{2})\mathrm{Rot}_x(\theta_1)\\ &R_2=\mathrm{Rot}_z(\frac{\pi}{2})\mathrm{Rot}_x(\theta_2) \end{aligned}\tag{2.15}$$ $$\begin{aligned} &F_1=R_1[0,0,f_1]^{\mathrm{T}},&M_1&=R_1[0,0,kf_1]^{\mathrm{T}}\\ &F_2=R_2[0,0,f_2]^{\mathrm{T}},&M_2&=R_2[0,0,-kf_2]^{\mathrm{T}}\\ \end{aligned}\tag{2.16}$$ $$\begin{aligned} &\boldsymbol{r}_1=[0,l_y,l_z]^{\mathrm{T}}\\ &\boldsymbol{r}_2=[0,-l_y,l_z]^{\mathrm{T}}\\ \end{aligned}\tag{2.17}$$

根据公式(1.12)和(1.13)可以得到：

$$\begin{aligned} &\boldsymbol{f}_b=\begin{bmatrix} f_1\mathrm{sin}\theta_1 + f_2\mathrm{sin}\theta_2\\ 0\\ f_1\mathrm{cos}\theta_1 + f_2\mathrm{cos}\theta_2 \end{bmatrix},\\ &\boldsymbol{\tau}_b=\begin{bmatrix} l_yf_1\mathrm{cos}\theta_1 - l_yf_2\mathrm{cos}\theta_2 + kf_1\mathrm{sin}\theta_1 - kf_2\mathrm{sin}\theta_2\\ l_zf_1\mathrm{sin}\theta_1 + l_zf_2\mathrm{sin}\theta_2\\ kf_1\mathrm{cos}\theta_1 - kf_2\mathrm{cos}\theta_2 - l_yf_1\mathrm{sin}\theta_1 + l_yf_2\mathrm{sin}\theta_2 \end{bmatrix} \end{aligned}\tag{2.18}$$

写成矩阵形式：

$$\begin{bmatrix} f_x\\ f_z\\ \tau_x\\ \tau_y\\ \tau_z \end{bmatrix}=\begin{bmatrix} 0&1&0&1\\ 1&0&1&0\\ l_y&k&-l_y&-k\\ 0&l_z&0&l_z\\ k&-l_y&-k&l_y \end{bmatrix}\begin{bmatrix} f_1\mathrm{cos}\theta_1\\ f_1\mathrm{sin}\theta_1\\ f_2\mathrm{cos}\theta_2\\ f_2\mathrm{sin}\theta_2\\ \end{bmatrix}\tag{2.19}$$

$f_x=f_1\mathrm{sin}\theta_1+f_2\mathrm{sin}\theta_2$为附加作用力，与tricopter类似，这里假设$f_x\approx0$。假设$l_z\neq0$(如果$l_z=0$将无法提供$y$方向的力矩)，解公式(2.19)可以得到的：

$$\begin{bmatrix} f_1\mathrm{cos}\theta_1\\ f_1\mathrm{sin}\theta_1\\ f_2\mathrm{cos}\theta_2\\ f_2\mathrm{sin}\theta_2\\ \end{bmatrix}=\frac{1}{2}\begin{bmatrix}1 & \frac{l_y}{k^{2} + l_y^{2}} & 0 & \frac{k}{k^{2} + l_y^{2}}\\ 0 & \frac{k}{k^{2} + l_y^{2}} & \frac{1}{l_z} & - \frac{l_y}{k^{2} + l_y^{2}}\\ 1 & - \frac{l_y}{k^{2} + l_y^{2}} & 0 & - \frac{k}{k^{2} + l_y^{2}}\\ 0 & - \frac{k}{k^{2} + l_y^{2}} & \frac{1}{l_z} & \frac{l_y}{k^{2} + l_y^{2}}\end{bmatrix}\begin{bmatrix} f_z\\ \tau_x\\ \tau_y\\ \tau_z \end{bmatrix}\tag{2.20}$$

 其余步骤参考四旋翼无人机的控制流程。

2.4 矢量共轴双旋翼

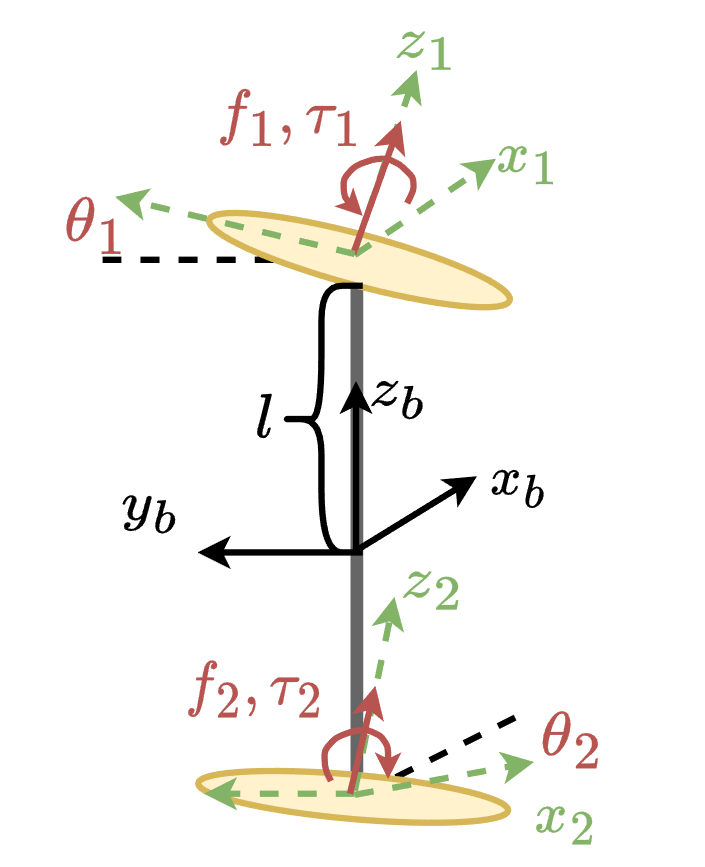
矢量共轴双旋翼的机构设计如图所示，可以列出：

$$\begin{aligned} R_1=\mathrm{Rot}_x(\theta_1)\\ R_2=\mathrm{Rot}_y(\theta_2) \end{aligned}\tag{2.21}$$ $$\begin{aligned} &F_1=R_1[0,0,f_1]^{\mathrm{T}},&M_1&=R_1[0,0,kf_1]^{\mathrm{T}}\\ &F_2=R_2[0,0,f_2]^{\mathrm{T}},&M_2&=R_2[0,0,-kf_2]^{\mathrm{T}}\\ \end{aligned}\tag{2.22}$$ $$\begin{aligned} &\boldsymbol{r}_1=[0,0,l]^{\mathrm{T}}\\ &\boldsymbol{r}_2=[0,0,-l]^{\mathrm{T}}\\ \end{aligned}\tag{2.23}$$

可以得到：

$$\boldsymbol{f}_b=\begin{bmatrix} f_2\mathrm{sin}\theta_2\\ -f_1\mathrm{sin}\theta_1\\ f_1\mathrm{cos}\theta_1 + f_2\mathrm{cos}\theta_2 \end{bmatrix}, \boldsymbol{\tau}_b=\begin{bmatrix} lf_1\mathrm{sin}\theta_1 - kf_2\mathrm{sin}\theta_2\\ -kf_1\mathrm{sin}\theta_1 - lf_2\mathrm{sin}\theta_2\\ kf_1\mathrm{cos}\theta_1 - kf_2\mathrm{cos}\theta_2 \end{bmatrix}\tag{2.24}$$

写成矩阵形式：

$$\begin{bmatrix} f_x\\ f_y\\ f_z\\ \tau_x\\ \tau_y\\ \tau_z \end{bmatrix}=\begin{bmatrix} 0&0&0&1\\ 0&-1&0&0\\ 1&0&1&0\\ 0&l&0&-k\\ 0&-k&0&-l\\ k&0&-k&0& \end{bmatrix}\begin{bmatrix} f_1\mathrm{cos}\theta_1\\ f_1\mathrm{sin}\theta_1\\ f_2\mathrm{cos}\theta_2\\ f_2\mathrm{sin}\theta_2 \end{bmatrix}\tag{2.25}$$

将$f_x$和$f_y$为附加作用力，与tricopter类似，这里假设$f_x,f_y\approx0$，解上式可以得到：

$$\begin{bmatrix} f_1\mathrm{cos}\theta_1\\ f_1\mathrm{sin}\theta_1\\ f_2\mathrm{cos}\theta_2\\ f_2\mathrm{sin}\theta_2 \end{bmatrix}=\begin{bmatrix}\frac{1}{2} & 0 & 0 & \frac{1}{2 k}\\0 & \frac{l}{k^{2} + l^{2}} & - \frac{k}{k^{2} + l^{2}} & 0\\\frac{1}{2} & 0 & 0 & - \frac{1}{2 k}\\0 & -\frac{k}{k^{2} +l^{2}} & -\frac{l}{k^{2} + l^{2}} & 0\end{bmatrix} \begin{bmatrix} f_z\\ \tau_x\\ \tau_y\\ \tau_z \end{bmatrix}\tag{2.26}$$

 其余步骤参考四旋翼无人机的控制流程。

3 全驱动无人机

3.1 全驱动倾转三旋翼

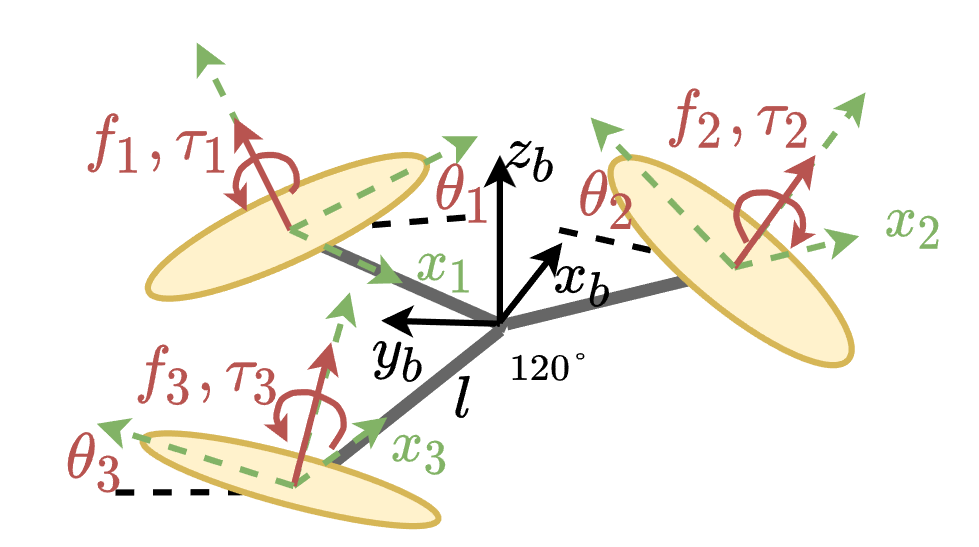
 三个旋翼的坐标系定义如图所示，三个旋翼都为倾转旋翼，倾转角度分别为$\theta_1,\theta_1,\theta_3$，机架为正三角形布置，机臂长为$l$。可以列出：

$$\begin{aligned} &R_1=\mathrm{Rot}_z(-\frac{2\pi}{3})\mathrm{Rot}_x(\theta_1)\\ &R_2=\mathrm{Rot}_z(-\frac{\pi}{3})\mathrm{Rot}_x(\theta_2)\\ &R_3=\mathrm{Rot}_x(\theta_3) \end{aligned}\tag{3.1}$$ $$\begin{aligned} &F_1=R_1[0,0,f_1]^{\mathrm{T}},&M_1&=R_1[0,0,kf_1]^{\mathrm{T}}\\ &F_2=R_2[0,0,f_2]^{\mathrm{T}},&M_2&=R_2[0,0,-kf_2]^{\mathrm{T}}\\ &F_3=R_3[0,0,f_3]^{\mathrm{T}},&M_3&=R_3[0,0,kf_3]^{\mathrm{T}}\\ \end{aligned}\tag{3.2}$$ $$\begin{aligned} &\boldsymbol{r}_1=\frac{1}{2}[l,\sqrt{3}l,0]^{\mathrm{T}}\\ &\boldsymbol{r}_2=\frac{1}{2}[l,-\sqrt{3}l,0]^{\mathrm{T}}\\ &\boldsymbol{r}_3=[-l,0,0]^{\mathrm{T}} \end{aligned}\tag{3.3}$$

根据公式(1.12)和(1.13)可以得到：

$$\begin{aligned} \boldsymbol{f}&=\begin{bmatrix} -\frac{\sqrt{3}}{2}f_1\mathrm{sin}\theta_1 - \frac{\sqrt{3}}{2}f_2\mathrm{sin}\theta_2\\ \frac{1}{2}f_1\mathrm{sin}\theta_1 - \frac{1}{2}f_2\mathrm{sin}\theta_2 - f_3\mathrm{sin}\theta_3\\ f_1\mathrm{cos}\theta_1 + f_2\mathrm{cos}\theta_2 + f_3\mathrm{cos}\theta_3 \end{bmatrix},\\ \boldsymbol{\tau}&=\begin{bmatrix} \frac{\sqrt{3}}{2}lf_1\mathrm{cos}\theta_1 - \frac{\sqrt{3}}{2}lf_2\mathrm{cos}\theta_2 - \frac{\sqrt{3}}{2}kf_1\mathrm{sin}\theta_1 + \frac{\sqrt{3}}{2}kf_2\mathrm{sin}\theta_2\\ -\frac{1}{2}lf_1\mathrm{cos}\theta_1 - \frac{1}{2}lf_2\mathrm{cos}\theta_2 + lf_3\mathrm{cos}\theta_3 + \frac{1}{2}kf_1\mathrm{sin}\theta_1 + \frac{1}{2}kf_2\mathrm{sin}\theta_2 - kf_3\mathrm{sin}\theta_3\\ kf_1\mathrm{cos}\theta_1 - kf_2\mathrm{cos}\theta_2 + kf_3\mathrm{cos}\theta_3 + lf_1\mathrm{sin}\theta_1 - lf_2\mathrm{sin}\theta_2 + lf_3\mathrm{sin}\theta_3 \end{bmatrix} \end{aligned}\tag{3.4}$$

写成矩阵形式：

$$\begin{bmatrix} f_x\\ f_y\\ f_z\\ \tau_x\\ \tau_y\\ \tau_z \end{bmatrix}=\begin{bmatrix} 0&-\frac{\sqrt{3}}{2}&0&-\frac{\sqrt{3}}{2}&0&0\\ 0&\frac{1}{2}&0&-\frac{1}{2}&0&-1\\ 1&0&1&0&1&0\\ \frac{\sqrt{3}}{2}l&-\frac{\sqrt{3}}{2}k&-\frac{\sqrt{3}}{2}l&\frac{\sqrt{3}}{2}k&0&0\\ -\frac{1}{2}l&\frac{1}{2}k&-\frac{1}{2}l&\frac{1}{2}k&l&-k\\ k&l&-k&-l&k&l \end{bmatrix}\begin{bmatrix} f_1\mathrm{cos}\theta_1\\ f_1\mathrm{sin}\theta_1\\ f_2\mathrm{cos}\theta_2\\ f_2\mathrm{sin}\theta_2\\ f_3\mathrm{cos}\theta_3\\ f_3\mathrm{sin}\theta_3\\ \end{bmatrix}\tag{3.5}$$

对上式求逆(可以使用sympy计算)可以得到：

$$\begin{bmatrix} f_1\mathrm{cos}\theta_1\\ f_1\mathrm{sin}\theta_1\\ f_2\mathrm{cos}\theta_2\\ f_2\mathrm{sin}\theta_2\\ f_3\mathrm{cos}\theta_3\\ f_3\mathrm{sin}\theta_3\\ \end{bmatrix}=\frac{1}{8k^2+9l^2}\begin{bmatrix}\frac{- 4 \sqrt{3} k^{3} - 3 \sqrt{3} k l^{2}}{3l} & \frac{4 k^{3} + 5 k l^{2}}{l} & 2 k^{2} + 3 l^{2} & \frac{4 \sqrt{3} k^{2} + 9 \sqrt{3} l^{2}}{3l} & \frac{- 4 k^{2} - 3 l^{2}}{l} & 2k\\ \frac{- 10 \sqrt{3} k^{2} - 9 \sqrt{3} l^{2}}{3} & 2 k^{2} + 3 l^{2} & -k l & -2\sqrt{3} k & -2k & 3 l\\ -\sqrt{3} k l & - k l & 4 k^{2} + 3 l^{2} & -3 \sqrt{3} l & -3 l & - 4 k\\ -2 \sqrt{3} k^{2} - 3 \sqrt{3} l^{2} &-2 k^{2} - 3 l^{2} &k l & 2\sqrt{3} k & 2k & -3 l\\ \frac{4\sqrt{3} k^{3} + 6\sqrt{3} k l^{2}}{3l} & \frac{- 4 k^{3} - 4 k l^{2}}{l} & 2 k^{2} + 3 l^{2} & - \frac{4 \sqrt{3} k^{2}}{3l} & \frac{4 k^{2} + 6 l^{2}}{l} & 2k\\ -\frac{2\sqrt{3} k^{2}}{3} & -6 k^{2} -6 l^{2} & -k l & -2\sqrt{3} k & -2k &3 l\end{bmatrix}\begin{bmatrix} f_x\\ f_y\\ f_z\\ \tau_x\\ \tau_y\\ \tau_z \end{bmatrix}\tag{3.6}$$

 全驱动无人机的自由度是完整的，$\boldsymbol{f}$和$\boldsymbol{\tau}$可以分别作为位置控制器和姿态控制器的控制输入。对于位置控制器，根据公式(1.6)设计$\boldsymbol{f}=MR^{\mathrm{T}}(-k_p\boldsymbol{e}-k_d\dot{\boldsymbol{\boldsymbol{e}}}+g\boldsymbol{e}_3-\boldsymbol{f}_e+\ddot{\boldsymbol{p}}_d) $。对于姿态控制器，可以参考 刚体姿态控制。

3.2 全驱动六旋翼

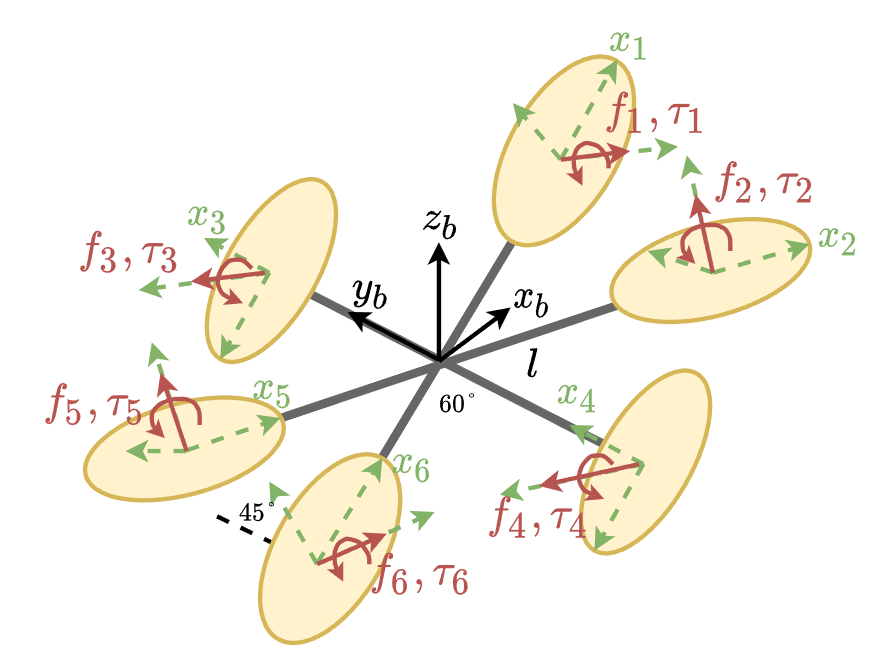
 六个固定旋翼的的坐标系定义如图所示，机架为正六边形布局，旋翼倾斜角为45度。可以列出：

$$\begin{aligned} &R_1=\mathrm{Rot}_z(\frac{\pi}{6})\mathrm{Rot}_x(\frac{\pi}{4})\\ &R_2=\mathrm{Rot}_z(-\frac{\pi}{6})\mathrm{Rot}_x(-\frac{\pi}{4})\\ &R_3=\mathrm{Rot}_z(\frac{\pi}{2})\mathrm{Rot}_x(-\frac{\pi}{4})\\ &R_4=\mathrm{Rot}_z(\frac{\pi}{2})\mathrm{Rot}_x(-\frac{\pi}{4})\\ &R_5=\mathrm{Rot}_z(-\frac{\pi}{6})\mathrm{Rot}_x(-\frac{\pi}{4})\\ &R_6=\mathrm{Rot}_z(\frac{\pi}{6})\mathrm{Rot}_x(\frac{\pi}{4})\\ \end{aligned}\tag{3.7}$$ $$\begin{aligned} &F_1=R_1[0,0,f_1]^{\mathrm{T}},&M_1&=R_1[0,0,kf_1]^{\mathrm{T}}\\ &F_2=R_2[0,0,f_2]^{\mathrm{T}},&M_2&=R_2[0,0,kf_2]^{\mathrm{T}}\\ &F_3=R_3[0,0,f_3]^{\mathrm{T}},&M_3&=R_3[0,0,kf_3]^{\mathrm{T}}\\ &F_4=R_4[0,0,f_4]^{\mathrm{T}},&M_4&=R_4[0,0,kf_4]^{\mathrm{T}}\\ &F_5=R_5[0,0,f_5]^{\mathrm{T}},&M_5&=R_5[0,0,kf_5]^{\mathrm{T}}\\ &F_6=R_6[0,0,f_6]^{\mathrm{T}},&M_6&=R_6[0,0,kf_6]^{\mathrm{T}}\\ \end{aligned}\tag{3.8}$$ $$\begin{aligned} &\boldsymbol{r}_1=\frac{l}{2}[\sqrt{3},1,0]^{\mathrm{T}}\\ &\boldsymbol{r}_2=\frac{l}{2}[\sqrt{3},-1,0]^{\mathrm{T}}\\ &\boldsymbol{r}_3=l[0,1,0]^{\mathrm{T}}\\ &\boldsymbol{r}_4=l[0,-1,0]^{\mathrm{T}}\\ &\boldsymbol{r}_5=\frac{l}{2}[-\sqrt{3},1,0]^{\mathrm{T}}\\ &\boldsymbol{r}_6=\frac{l}{2}[-\sqrt{3},-1,0]^{\mathrm{T}} \end{aligned}\tag{3.9}$$

根据公式(1.12)和(1.13)可以得到：

$$\begin{aligned} &\boldsymbol{f}=\begin{bmatrix} \frac{\sqrt{2}}{4}&&\\ &\frac{\sqrt{6}}{4}&\\ &&\frac{\sqrt{2}}{2} \end{bmatrix} \begin{bmatrix} f_1+f_2-2f_3-2f_4+f_5+f_6\\ -f_1+f_2+f_5-f_6\\ f_1+f_2+f_3+f_4+f_5+f_6 \end{bmatrix}\\ &\boldsymbol{\tau}=\begin{bmatrix} \frac{\sqrt{2}}{4}&&\\ &\frac{\sqrt{6}}{4}&\\ &&\frac{\sqrt{2}}{2} \end{bmatrix} \begin{bmatrix} (l+k)f_1-(l-k)f_2+2(l-k)f_3-2(l+k)f_4+(l+k)f_5-(l-k)f_6 \\ -(l+k)f_1-(l-k)f_2+(l+k)f_5+ (l-k)f_6\\ -(l-k)f_1+(l+k)f_2+(l+k)f_3-(l-k)f_4-(l-k)f_5+(l+k)f_6 \end{bmatrix}\\ \end{aligned}\tag{3.10}$$

写成矩阵形式：

$$\begin{bmatrix} f_x\\ f_y\\ f_z\\ \tau_x\\ \tau_y\\ \tau_z \end{bmatrix}=\begin{bmatrix} \frac{\sqrt{2}}{4}&\frac{\sqrt{2}}{4}&-\frac{\sqrt{2}}{2}&-\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{4}&\frac{\sqrt{2}}{4}\\ -\frac{\sqrt{6}}{4}&\frac{\sqrt{6}}{4}&0&0&\frac{\sqrt{6}}{4}&-\frac{\sqrt{6}}{4}\\ \frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{4}(l+k)&-\frac{\sqrt{2}}{4}(l-k)&\frac{\sqrt{2}}{2}(l-k)&-\frac{\sqrt{2}}{2}(l+k)&\frac{\sqrt{2}}{4}(l+k)&-\frac{\sqrt{2}}{4}(l-k)\\ -\frac{\sqrt{6}}{4}(l+k)&-\frac{\sqrt{6}}{4}(l-k)&0&0&\frac{\sqrt{6}}{4}(l+k)&\frac{\sqrt{6}}{4}(l-k)\\ -\frac{\sqrt{2}}{2}(l-k)&\frac{\sqrt{2}}{2}(l+k)&\frac{\sqrt{2}}{2}(l+k)&-\frac{\sqrt{2}}{2}(l-k)&-\frac{\sqrt{2}}{2}(l-k)&\frac{\sqrt{2}}{2}(l+k) \end{bmatrix}\begin{bmatrix} f_1\\ f_2\\ f_3\\ f_4\\ f_5\\ f_6\\ \end{bmatrix}\tag{3.11}$$

对公式(3.11)求逆可以得到：

$$\begin{bmatrix} f_1\\ f_2\\ f_3\\ f_4\\ f_5\\ f_6\\ \end{bmatrix}=\frac{\sqrt{2}}{6l}\begin{bmatrix} l-k&-\sqrt{3}(l-k)&l+k&1&-\sqrt{3}&-1\\ l+k&\sqrt{3}(l+k)&l-k&-1&-\sqrt{3}&1\\ -2(l+k)&0&l-k&2&0&1\\ -2(l-k)&0&l+k&-2&0&-1\\ l-k&\sqrt{3}(l-k)&l+k&1&\sqrt{3}&-1\\ l+k&-\sqrt{3}(l+k)&l-k&-1&\sqrt{3}&1 \end{bmatrix}\begin{bmatrix} f_x\\ f_y\\ f_z\\ \tau_x\\ \tau_y\\ \tau_z \end{bmatrix}\tag{3.12}$$

 与全驱动倾转三旋翼类似，全驱动三旋翼的自由度是完整的，控制器的设计可参考3.1中的步骤。

4 补充

 前面讨论了不同构型的无人机的基本控制，中间有一些可能需要解决的问题比较复杂，没有进行讨论，在这里列出：

• 混控关系的可逆性：这里以常见的平面六旋翼无人机为例，六旋翼无人机有$6$个可以驱动的旋翼，推导混控矩阵时会发现混控矩阵是一个$6\times6$的方阵，但是这个方阵的秩为$4$，是不可逆的，也就是说平面六旋翼无人机只有4个可以独立驱动的自由度。因此，如果想要设计一个全驱动的无人机，如何优化无人机的旋翼布局保证混控矩阵的可逆性，是一个需要考虑的问题。如果只考虑平面六旋翼4个可以独立驱动的自由度，以4个驱动力或力矩来求取6个旋翼的升力，会发现有无穷多个解，也就是说，如果无人机只驱动这四个自由度，旋翼的数量是冗余的。对于冗余的自由度，如何充分利用也是一个需要考虑的问题，例如如何用冗余的自由度应对旋翼故障，或是将部分控制任务放在0空间中，实现子任务和优先级控制。
• 奇异性：考虑一个完整驱动的无人机，虽然旋翼能够提供机体坐标系下的完整驱动力和力矩，但是可能存在一种情况：无人机在某个姿态下所提供的最大升力无法克服重力，使得无人机无法到达所有的姿态空间。因此，如何优化旋翼布局，避免这种奇异的出现或是最大化可到达的姿态空间是一个需要考虑的问题。此外，对于多组倾斜旋翼构成的无人机而言，旋翼的产生的气流有比较大的交叉和重叠，效率是比较低的，如何在保证驱动自由度的情况下，如何通过旋翼布局最大化驱动效率也是一个问题。
• 抗扰动控制：文中的控制器并未对扰动进行补偿，当系统中存在有界扰动时，会有较大的跟踪静差。可以设计自适应率，或者在控制器中加入积分环节进行补偿。
• 倾转旋翼的动力学对于带有倾转旋翼的无人机，应其动力学该是一个多体动力学模型，当简化成单一刚体进行建模和控制，会导致很多未建模的不确定性，特别是旋翼的质量惯量、空气动力学不可忽略，倾转电机的响应速度有限的情况下，简化的建模容易导致调参困难，运动性能无法调节地较为激进，甚至控制失效等问题。